The Hyperbolic Games are similar in spirit to the Torus Games, but played on curved surfaces. Most people will want to start with the Torus Games instead, which offer a selection of easily playable games, designed for children ages 10 and up, all implemented in multi-connected spaces in 2 and 3 dimensions.
The Hyperbolic Games, by contrast, are for math students — advanced undergraduates and beginning graduate students. These games are more challenging than the Torus Games because they combine a multi-connected topology with a non-Euclidean geometry. Mathematically they illustrate the following:
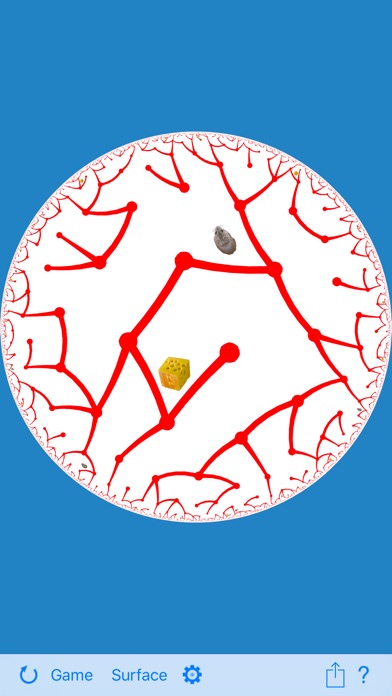
- The hyperbolic plane, as a live scrollable object.
- The under-appreciated fact that the two traditional models of the hyperbolic plane are simply different views of the same fixed-radius surface in Minkowski space: the Beltrami-Klein model corresponds to a viewpoint at the origin (central projection) while the Poincaré disk model corresponds to a viewpoint one radian further back (stereographic projection). Players may pinch-to-zoom to pass from one to the other, or stop to view the model from any other distance.
- The strong — but also under-appreciated — correspondence between the hyperbolic plane and an ordinary sphere. In particular, central projection of the sphere corresponds to the Beltrami-Klein model of the hyperbolic plane, and stereographic projection of the sphere corresponds to the Poincaré disk model of the hyperbolic plane.
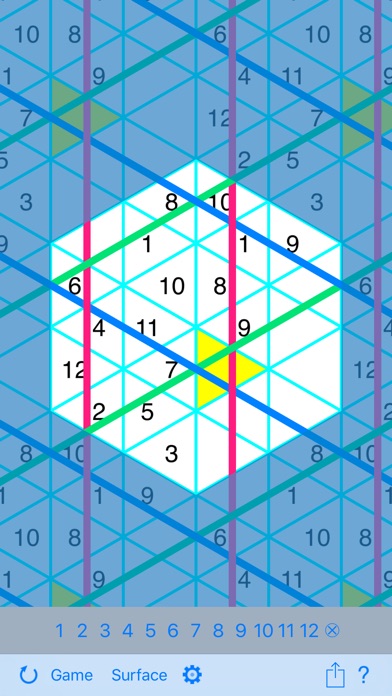
- The Klein quartic surface, viewed with its natural geometry. The sudoku puzzles take full advantage of the Klein quartic’s tremendous amount of symmetry.